What is idempotence?

If you frown after reading idempotence, don’t worry. Although this word sounds unusual it conceals a simple mathematics property. Needless to say, this characteristic has also a big meaning in Computer Science.
Idempotence operation is an operation that can be applied multiple times without changing the result beyond the initial application. It may sound difficult but after a couple of examples, the general concept will be obvious.
To be honest, I spent a lot of time looking for proper examples of idempotent functions or operations. Although I caught the idempotence concept very fast, I wanted to go deeper. I tried to understand not only what it is but also why does it matter. I’ll share my thoughts on this article.
Idempotence in mathematics
In math, each function produces a certain output. This is the reason why we ever use functions – we pass input arguments and we expect an output value. If we pass the same argument, again and again, each time we’ll get the same output. It means that math functions are pure – their output depends only on the input arguments.
$$f(x) = y$$
Now, imagine that we call the function with a certain argument. It produces a specific output depends on the input value. Let’s call the function again, but for the input value, use the result from the previous execution.
Idempotent functions
If the output doesn’t change anymore, the function is idempotent. Only the first execution of function produces a new value. Each subsequent call returns the same value, no matter how many times we call the function. In other words, the function fulfills below equation.
$$f(f(x)) == f(x)$$
Do you know the example of an often used idempotent function? The well-knowing example is the absolute value. For each negative value as an input abs returns its positive counterpart. For each positive value, it returns input argument as is.
$$abs(abs(-5)) == abs(-5)$$
Pure function and idempotent function are not the same. Function can be pure, but not idempotent, e.g.
f(x) = x + 1. Essentially, f(x) is pure because its output depends only on the input argument. But it’s not idempotent because it not fulfills the conditionf(f(x)) == f(x).
Idempotent operations
Under certain conditions, we can recognize some mathematical operations as an idempotent. Take a look at these two binary operations: addition and multiplication. They are not fully idempotent. But if one of the argument is an identity element, the operation is idempotent.
-
For addition, the identity element is equal to 0 (zero). Whatever adds to zero, we’ll get the same value.
$$5 + 0 = 5$$
-
For multiplication, the identity element is equal to 1 (one). Something times one always returns that “something”.
$$5 * 1 = 5$$
It doesn’t matter how many times we’ll perform the operation with identity element in the pair. Each time we’ll get the same output.
Idempotence in programming
In programming, we have a lot of pure and idempotent functions in mathematical sense, e.g.
- floor / ceil
- lowercase / uppercase
- trim
In many programming languages, functions do much more operations beside returning an output. Sometimes they return nothing. Another time they return different results, although we use the same input arguments.
But why? What is the difference between the mathematical function and the programming languages functions?
Side effects
Of course, we can place maths functions within our program and everything will be fine. But in most cases, we use functions to manage the state. These functions that depend not only on the input arguments. They also use something outside its local scope (e.g. global state) so they are no longer pure – they have side effects.
The function has side effects when
- it reads or modifies the global state
- writes or reads data from I/O or database
- uses a timestamp, current date
- uses something that has effects beyond it
But side effects doesn’t exclude function to be idempotent. We’ll take a closer look at the non-pure but idempotent function.
Idempotent functions in programming
In programming, a function is idempotent, when we can call it many times with the same arguments and the result won’t change beyond initial calling.
It is close enough to the mathematical definition but instead of applying function, we execute it many times.
Let’s assume, we have an array of figures. Now, we’ll sort this array in PHP language. Please notice, that PHP’s sort function expected input array as a reference. That means, it modifies the variable outside its scope, so the sort function has the side effect.
$numbers = [3, 4, 2, 5, 1];
sort($numbers); // [1, 2, 3, 4, 5]
sort($numbers); // [1, 2, 3, 4, 5]
sort($numbers); // [1, 2, 3, 4, 5]
It doesn’t matter how many times we’ll call a sort function. We’ll always get the same outcome. The same for well-knowing setters.
$person = new Person("Simon");
$person->setName("Szymon");
$person->setName("Szymon");
$person->setName("Szymon");
Only the first call of setter will change the name. If we use it many times, even by mistake, nothing bad will happen.
Idempotence in HTTP
Idempotence plays a big role in HTTP protocol. Lots of web browsers lead to the concept of idempotency and the assumption which HTTP methods are idempotent and safe. According to the official HTTP specification, GET and HEAD should be considered as safe methods. Moreover, GET, HEAD, PUT, DELETE, OPTIONS, and TRACE should be considered as idempotent methods.
Thinking in REST
Let’s assume, that we have a resource. When we read from it, nothing dangers should happen. This is exactly how GET method works. It should only read from the server and that’s why it’s safe.
Please note, that we talk about the official HTTP/1.1 specification. Everyone could implement these methods differently, according to own needs.
Now, let’s consider a PUT method. This is idempotent operation. Only the first request should affect our resource. If we’ll send an extra request with the same data, nothing destructive should happen, because data is replaced, rather than appended.
DELETE is also interesting. The first DELETE request is obvious – it deletes the resource from the server. But each next DELETE request to the same resource should be ignored. The server should respond to the client by the specific code, e.g. 404. That makes this request idempotent.
But not all HTTP methods work in this way. Let’s take a look at the POST method. This method is neither idempotent nor safe. It creates the new entity within the resource, identifiable by a unique id. Each subsequent POST request will be creating the new entity with completely new identity, so this method isn’t idempotent.
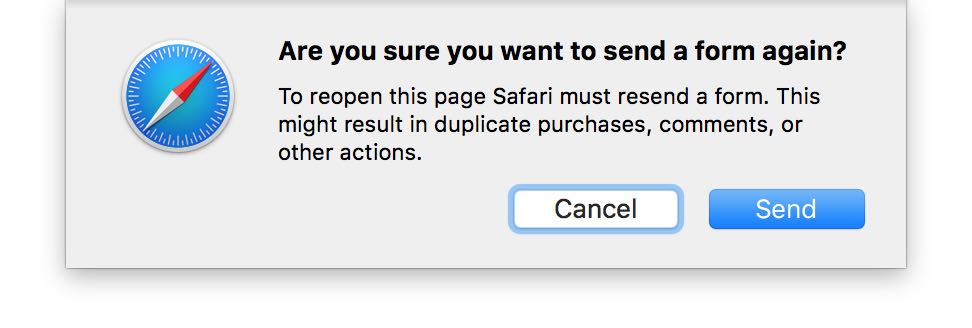
It’s so important that even web browsers show an alert in the case when we try to resend before processed form. Thanks to the HTTP/1.1 – RFC 2616, each browser handles all methods in the same way.
Conclusions
Idempotence is not a magic tool that we should use to build better things. It’s a property of some functions and operations that protect us from errors caused by repetition. Very often we don’t even need this characteristic within your own functions. That’s O.K. Idempotence plays a big role not only in math and computer science but also in the real world and it often went unnoticed.
Did you notice the featured image? What will happen if we press the same button in an elevator again? In elevators I know, nothing will happen. The floor will be still highlighted and the elevator does its work.
Buttons at pedestrian crossing work in the same way. It doesn’t matter how long you keep it pressed or how many times you push it. The very first call (in each cycle, of course) is important.

If you select the current channel on your remote, the TV will do nothing.
Some cars have a remote with two buttons dedicated to opening and closing a car. If you open the opened car, it’ll be still opened. That’s obvious.
Do you know other examples? As you see, they are everywhere but I thought long before I found some good ones. Idempotence isn’t so important in our daily work but is worth-knowing property if you use the functional paradigm. Now you know why.
Resources
- Idempotence – Wikipedia
- RFC 2616 – Hypertext Transfer Protocol – HTTP/1.1
- Eric Evans, Domain-Driven Design: Tackling Complexity in the Heart of Software, Side-effect-free functions, (Polish edition)